Research

Quantum metrology and sensing

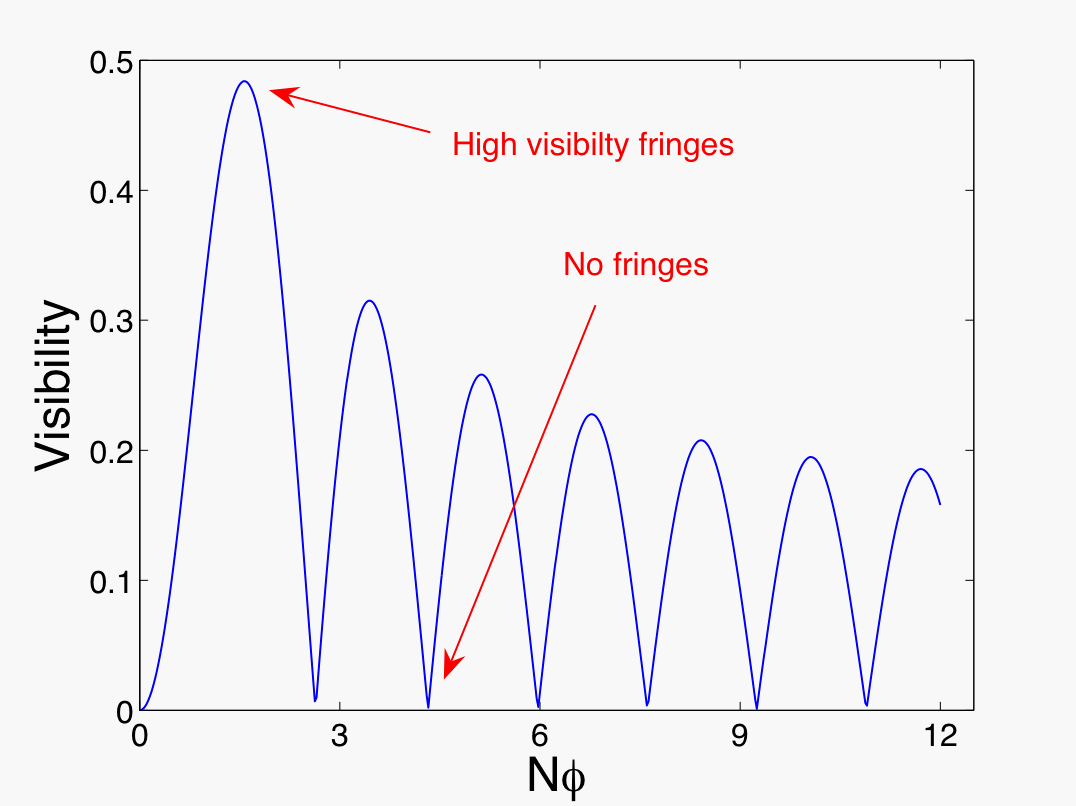
The ability to detect and measure physical phenomena with ever-greater sensitivity is an important technological challenge. Not only does it allow us to subject scientific theories to higher levels of scrutiny, but is important for new commercial applications such as clocks, sensors and navigation systems. Current sensors rely on conventional (classical) physics. However, by using a fully quantum approach it is possible to achieve much greater sensitivities to phenomena such as magnetic, electric, or gravitational fields or rotations. The feasibility of these ideas has been demonstrated in principle in atomic and optical systems however there are still a number of important open questions about the applicability and practicality of quantum-enhanced sensing. We are working on designing practical schemes for devices such as quantum-enhanced gyroscopes and investigating key questions such as when does it help to have a network of entangled sensors and how do we deal with nuisance parameters (such as a misalignment between our gyroscopes). We are also studying the formalism of metrology to understand the limitations of the Cramer-Rao bound when we do not have sufficient measurements and how to properly account for any prior information we may have.

1. J.A. Dunningham, Contemp. Phys. 47, 257 (2006) Link
2. J.A. Dunningham and K. Burnett, Physical Review A 70, 033601 (2004) Link
3. J.A. Dunningham, K. Burnett, and S.M. Barnett, Physical Review Letters 89, 150401 (2002) Link
4. T. J. Proctor, P. A. Knott and J. A. Dunningham, arXiv:1702.04271 Link
5. P. Kok, J. Dunningham and J.F. Ralph, Phys. Rev. A 95, 012326 (2017) Link

back to the top

Foundations of Quantum Mechanics

• Emergence of classical observables from the quantum world

Developing a Firm Position

Science 301: 1013a.

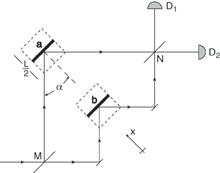In the classical world, the position of an object is well defined, but in quantum mechanics, increasing the precision of position measurement comes at the expense of losing information about the particle's momentum. This difference is well accepted, but it is still important to understand how larger objects that are made up on quantum-mechanical particles can develop their "classical" properties. Taking an approach that views position as a relative measurement, Rau et al. (see paper) present a thought experiment that shows how two particles, when subjected to a series of scattering interactions in which they become progressively more entangled, should localize in space with a well-defined separation. The proposal suggests that localization and the emergence of the classical world can be understood in terms of entanglement.

Science, Volume 301, Number 5636, Issue of 22 Aug 2003, p. 1013.
Copyright © 2003 by The American Association for the Advancement of Science. All rights reserved.

---

• Macroscopic superposition states

Work featured in the cover article of New Scientist issue 2595, 17 March 2007, page 36-39

How to make a fat cat

Schrödinger cats - macroscopic objects in "superpositions" of different quantum states - are hard to make. If they weren't, chairs and tables and you and I could be in multiple places at once. Now David Hallwood and Keith Burnett of the University of Oxford and Jacob Dunningham of the University of Leeds, UK, have come up with a recipe for researchers. They imagine a bucket filled with a bunch of supercooled atoms all in the same quantum state, known as a Bose-Einstein condensate. One of the strange properties of this state of matter is that all the atoms remain stationary when you rotate the bucket, rather than move with it. From the bucket's point of view, however, the atoms revolve in the opposite direction. Similarly, if the atoms are in an excited state where they all revolve at the same speed, you can rotate the bucket so that from its view the atoms are not moving. Finally, imagine rotating the bucket at some intermediate speed so that the stationary atoms and the excited atoms have the same speed but are revolving in opposite directions from the bucket's point of view. Those are your states of superposition. "The system doesn't know what state to pick," says Hallwood. In order to make a fat cat, the energies of the two states need to be similar, and there cannot be others close by in energy. The states must also have a high probability of making the transition from one to the other, but a low probability of going to any other states. This recipe could be useful for building superconducting devices.

---

• Generalised uncertainty relations

Together with Petr Jizba at CTU in Prague I have been developing generalised uncertainty relations based on the concept of entropy power. We have derived a new one-parameter class of information-theoretic uncertainty relations for pairs of conjugate observables in an infinite-dimensional Hilbert space. This class constitutes an infinite family of higher-order statistics uncertainty relations, which allows one in principle to determine the shape of the underlying information-distribution function by measuring the relevant entropy powers. The familiar Robertson-Schrödinger uncertainty relation is a special case of this, but the full family of relations is much more information-rich and yields interesting details of the underlying structure of the quantum states.

1. Petr Jizba, Yue Ma, Anthony Hayes and Jacob A. Dunningham, Physical Review E (Rapid) 93, 060104(R) (2016). Link
2. P. Jizba, J.A. Dunningham and J. Joo, Annals of Physics 355, 87 (2015). Link

---

• Single particle entanglement

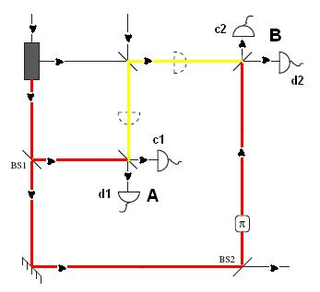
Feynman famously claimed that superposition is the only mystery in quantum mechanics. Others might add nonlocality. If, however, single particles can exhibit nonlocality, then these two mysteries become one and the same. This is an important issue since, in quantum field theory, excitations rather than particles are the most fundamental entities. There would be a problem if nonlocality only existed when we had two or more particles, since there would be something peculiar about two excitations that would not exist when we had only one. There has been a great deal of debate about whether it is possible for a single photon to exhibit nonlocality. A number of schemes have been proposed that claim to demonstrate this effect, but objectors claim that they do not represent experiments that could actually be performed. Dunningham and Vedral have shown how it is possible to overcome these objections by presenting an experimentally feasible scheme. Furthermore, all the techniques required for photons are equally applicable to atoms. It should, therefore, also be possible to use their scheme to verify the nonlocality of a single massive particle.

Jacob Dunningham and Vlatko Vedral Physical Review Letters 99, 180404 (2007) Link
Also featured on PhysOrg.com Link

back to the top

Theory of Bose-Einstein condensates

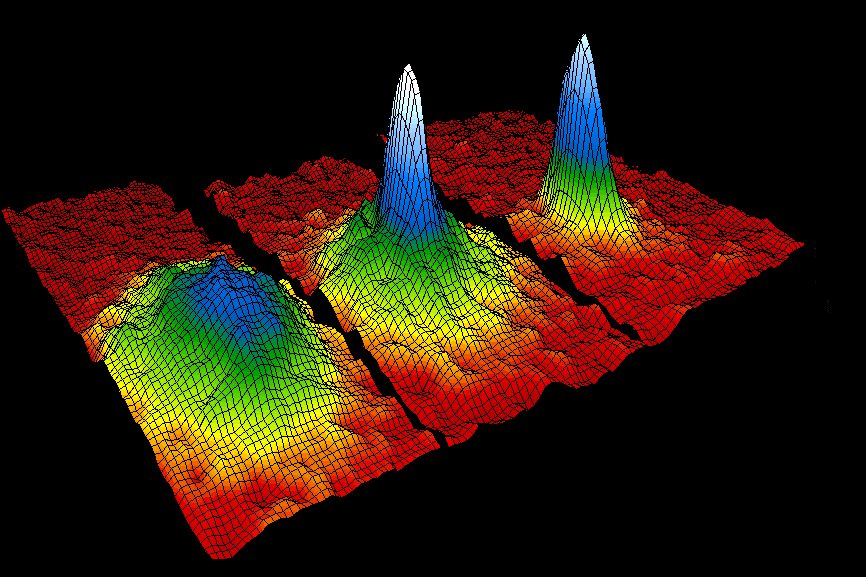
I am interested in the critical behaviour of atoms at low temperatures known as Bose-Einstein condensation (BEC). This is a fascinating macroscopic manifestation of quantum mechanics that was predicted by Albert Einstein in the 1920s (based on the work of S.N. Bose) and first observed in dilute atomic systems in 1995. In addition to exploring the physics behind this phenomenon, I also investigate quantum information processing using BECs. My research extends into other low temperature phenomena, such as superconductivity, and its relation to entanglement in general.

back to the top